
Q. Five jobs (J1, J2, J3, J4 and J5) need to be processed in a factory. Each job can be assigned to any of the five different machines (M1, M2, M3, M4 and M5). The time durations taken (in minutes) by the machines for each of the jobs, are given in the table. However, each job is assigned to a specific machine in such a way that the total processing time is minimum. The total processing time is ____________minutes.
| M1 | M2 | M3 | M4 | M5 | |
| J1 | 40 | 30 | 50 | 50 | 58 |
| J2 | 26 | 38 | 60 | 26 | 38 |
| J3 | 40 | 34 | 28 | 24 | 30 |
| J4 | 28 | 40 | 40 | 32 | 48 |
| J5 | 28 | 32 | 38 | 22 | 44 |
Ans:
Subtracting minimum value of each row from corresponding row elements.
| M1 | M2 | M3 | M4 | M5 | |
| J1 | 10 | 0 | 20 | 20 | 28 |
| J2 | 0 | 12 | 34 | 0 | 12 |
| J3 | 16 | 10 | 4 | 0 | 6 |
| J4 | 0 | 12 | 12 | 4 | 20 |
| J5 | 6 | 10 | 16 | 0 | 22 |
Subtracting minimum value of each column from corresponding column.
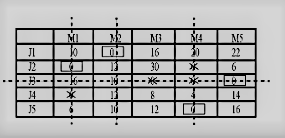
Now Number of assignments is less than the number of machines. Hence current solution is not optimal. Now adding minimum uncovered value at all junctions and subtracting from uncovered values.
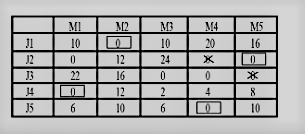
Hence,
Job 1 → Machine 2
Job 2 → Machine 5
Job 3 → Machine 3
Job 4 → Machine 1
Job 5 → Machine 4
Total time = 30 + 38 + 28 + 28 + 22 = 146



![Determine the correctness (or otherwise) of the following Assertion [A] and the Reason [R]](https://www.gkseries.com/blog/wp-content/uploads/2023/10/Determine-the-correctness-or-otherwise-of-the-following-Assertion-A-and-the-Reason-R.jpg)
