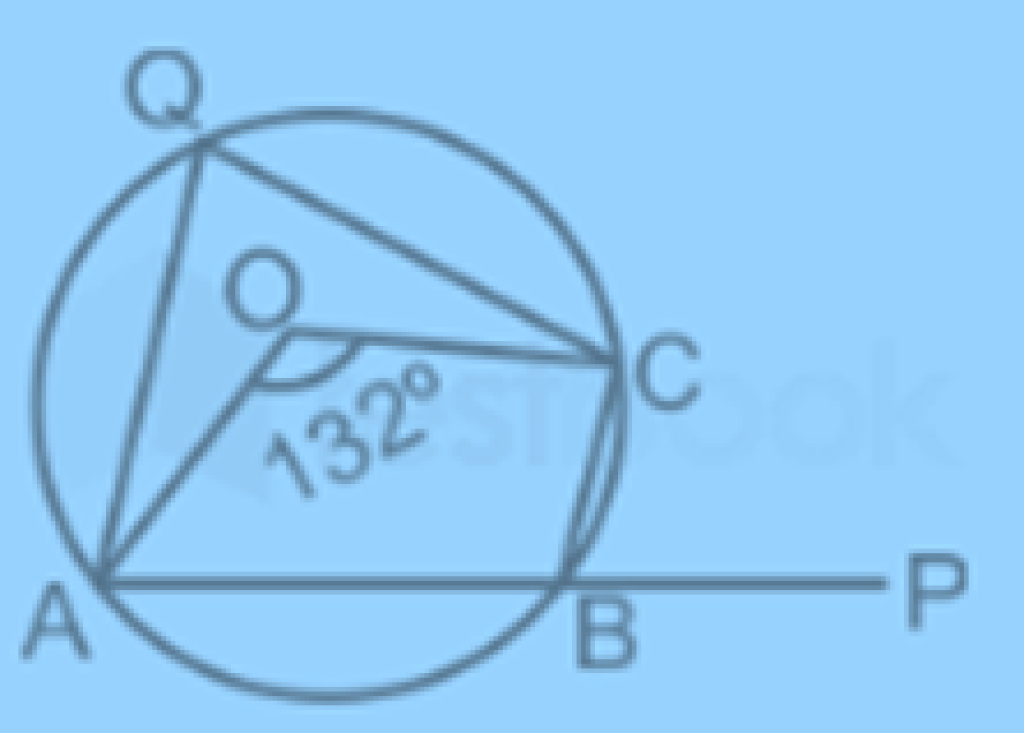
In a circle with center O, an arc ABC subtends an angle of 132 degree at the center of the circle. Chord AB is produced to

In a circle with center O, an arc ABC subtends an angle of 132 degree at the center of the circle. Chord AB is produced to point P, find angle CBP

(a) 48

(b) 68

(c) 66

(d) 76

Sol:

As we know

The angle subtended by an arc at the centre of a circle is double the size of the angle subtended by the same arc at the circle circumference 

Take any point Q on the circumference and join AQ and QC. 

∴ ∠AOC = 2 × ∠AQC 

⇒ ∠AQC = 1/2 × ∠AOC = 1/2 × 132° = 66° 

Now, ∠CBP = ∠AQC   [Exterior angle of cyclic quadrilateral] 

⇒ ∠CBP = 66°